简介
这篇论文是令我印象深刻的几篇关于MIT Cheetah的论文。除此之外还有MIT Cheetah 3提出使用凸优化的方法达到很好的动态控制效果，也算是我正式理解了四足动态控制的关键点。还有一篇就是Mini Cheetah的论文，它提出了低成本的四足机器人方案，在国内可以在1W5左右的成本做出一台四足机器人。
这篇论文第一章是Introduction，介绍了各种四足的控制方法，包括SLIP、WBC、MPC、Nonlinear TO、RL等。
理论与模型定义
第二章开始文章主体部分，从机器人理论建模开始。
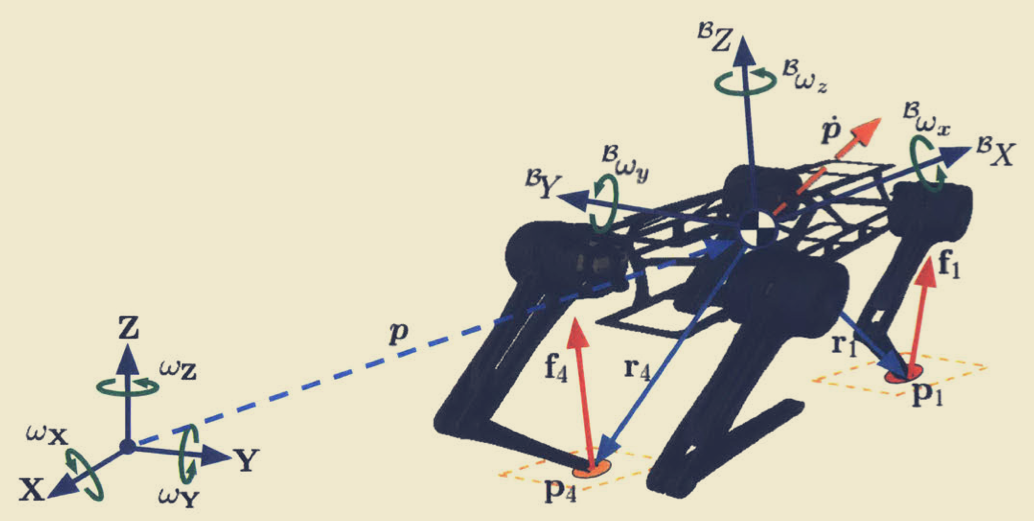
机器人的质心(CoM)表示为：
p = [ p x p y p z ] \bold{p} = \left[ \begin{array}{l} p_x \\ p_y \\ p_z \end{array} \right]
p = ⎣ ⎢ ⎡ p x p y p z ⎦ ⎥ ⎤
机器人的质心速度表示为：
p ˙ = [ p x ˙ p y ˙ p z ˙ ] \dot{\bold{p}} = \left[ \begin{array}{l} \dot{p_x} \\ \dot{p_y} \\ \dot{p_z} \end{array} \right]
p ˙ = ⎣ ⎢ ⎡ p x ˙ p y ˙ p z ˙ ⎦ ⎥ ⎤
B p ˙ = [ B p x ˙ B p y ˙ B p z ˙ ] ^{B}\dot{\bold{p}} = \left[ \begin{array}{l} ^{B}\dot{p_x} \\ ^{B}\dot{p_y} \\ ^{B}\dot{p_z} \end{array} \right]
B p ˙ = ⎣ ⎢ ⎡ B p x ˙ B p y ˙ B p z ˙ ⎦ ⎥ ⎤
p ˙ = I R B B p ˙ \dot{\bold{p}} = ^{I}\bold{R}_{B} \\ ^{B}\dot{\bold{p}}
p ˙ = I R B B p ˙
对于机器人的身体旋转表示，文章中提到了三种方法，分别是欧拉角、四元数和旋转矩阵。本文中用到的主要与控制相关的方法是欧拉角。
欧拉角表示如下：
Θ = [ θ ϕ ψ ] \bold{\Theta} = \left[ \begin{array}{l} \theta \\ \phi \\ \psi \end{array} \right]
Θ = ⎣ ⎢ ⎡ θ ϕ ψ ⎦ ⎥ ⎤
Θ ˙ = [ θ ˙ ϕ ˙ ψ ˙ ] \dot{\bold{\Theta}} = \left[ \begin{array}{l} \dot{\theta} \\ \dot{\phi} \\ \dot{\psi} \end{array} \right]
Θ ˙ = ⎣ ⎢ ⎡ θ ˙ ϕ ˙ ψ ˙ ⎦ ⎥ ⎤
四元数表示如下：
q ˙ = [ q r q i q j q k ] \dot{\bold{q}} = \left[ \begin{array}{l} q_r \\ q_i \\ q_j \\ q_k \end{array} \right]
q ˙ = ⎣ ⎢ ⎢ ⎢ ⎡ q r q i q j q k ⎦ ⎥ ⎥ ⎥ ⎤
旋转矩阵相关的计算如下：
I R ˙ B = I R B [ B ω ] × ^{I}\dot{\bold{R}}_{B} = ^{I}\bold{R}_{B} [^{B}\omega]_{\times}
I R ˙ B = I R B [ B ω ] ×
腿部的关节与足部末端的定义如下：
q ˙ = [ q i , A b / A d q i , h i p q i , k n e e ] p = [ p i , x p i , y p i , z ] \dot{\bold{q}} = \left[ \begin{array}{l} q_{i,Ab/Ad} \\ q_{i,hip} \\ q_{i,knee} \end{array} \right] \bold{p} = \left[ \begin{array}{l} p_{i,x} \\ p_{i,y} \\ p_{i,z} \end{array} \right]
q ˙ = ⎣ ⎢ ⎡ q i , A b / A d q i , h i p q i , k n e e ⎦ ⎥ ⎤ p = ⎣ ⎢ ⎡ p i , x p i , y p i , z ⎦ ⎥ ⎤
控制架构
控制结构如下图所示，通过手柄输入期望的控制，经过控制器解算后得到机器人的关节控制力矩。其中摆动腿与支撑腿用不同的控制方法，支撑腿用力控制，摆动腿用带补偿的PD控制。
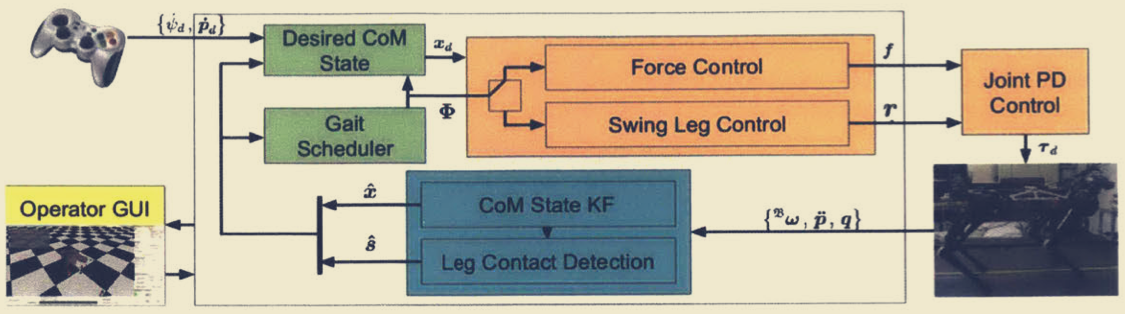
状态估计
MIT这个机器人控制中，很重要的一个部分就是通过机器人的本体传感器，包括关节力矩传感器和IMU，不额外加视觉等传感器，机器人通过估计算法准确的得知机器人当前状态。我记得最早的四足相关的状态估计的论文是ETH出的，使用EKF进行估计，本文进行化简后，可以直接使用Kalman Filter进行状态估计。
状态转移函数如下
p ˙ = v \dot{\bold{{p}}} = \bold{v}
p ˙ = v
v ˙ = I R ˙ B b a + g + ω v \dot{\bold{v}} = ^{I}\dot{\bold{R}}_{B} \\ ^{b}a + \bold{g} + \bold{\omega}_v
v ˙ = I R ˙ B b a + g + ω v
p ˙ i = ω ˙ p i \dot{\bold{p}}_{i} = \dot{\bold{\omega}}_{p_i}
p ˙ i = ω ˙ p i
在后续文章里，我会补充关于Kalman Filer部分的公式。这里的基本思想就是，依靠支撑腿与IMU结合来估计身体的速度姿态等信息。
腿部控制
摆动腿控制
τ F F , i = J i T Λ i ( B a i , r e f − J ˙ i a ˙ i ) + C i q ˙ i + G i \bold{\tau}_{FF,i} = \bold{J}^{T}_{i} \Lambda_i (^{B}a_{i,ref} - \dot{\bold{J}}_i \dot{\bold{a}}_i) + \bold{C}_i \dot{\bold{q}}_i + \bold{G}_i
τ F F , i = J i T Λ i ( B a i , r e f − J ˙ i a ˙ i ) + C i q ˙ i + G i
τ F B , i = J i T [ K p ( B p i , r e f − B p i ) + K d ( B v i , r e f − B v i ) ] \bold{\tau}_{FB,i} = \bold{J}^{T}_{i}[ \bold{K}_p (^{B}\bold{p}_{i,ref} - ^{B}\bold{p}_i) + \bold{K}_d (^{B}\bold{v}_{i,ref} - ^{B}\bold{v}_i)]
τ F B , i = J i T [ K p ( B p i , r e f − B p i ) + K d ( B v i , r e f − B v i ) ]
τ i = τ F F , i + τ F B , i \bold{\tau}_i = \bold{\tau}_{FF,i} + \bold{\tau}_{FB,i}
τ i = τ F F , i + τ F B , i
支撑腿力控制
τ i = J i T f i \bold{\tau}_i = \bold{J}^{T}_{i} \bold{f}_i
τ i = J i T f i
步态规划
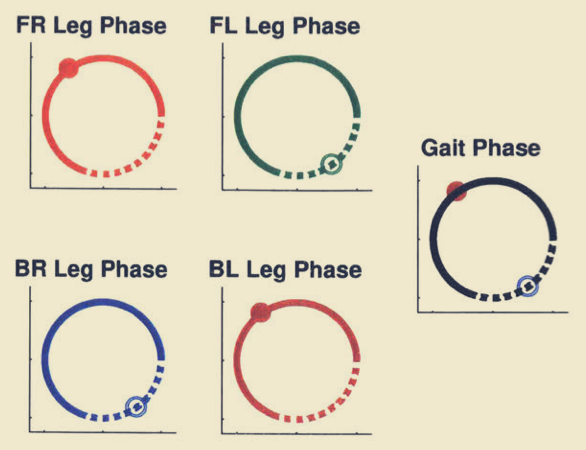
这篇论文使用步态相位这种方法来定义步态，通过这种方法可以直接用统一的参数定义比如Trot、Gallop、Walk等步态。论文使用下述参数来计算当前腿的相位或者是状态。这是一个很巧妙的办法，我个人觉得这种方法可以用在强化学习中，作为某种待优化的参数，来使机器人学习到更好的控制策略。
Φ i = m o d ( t − t 0 , i T p , 1 ) \Phi_i = mod \left( \tfrac{t-t_{0,i}}{T_p} , 1 \right)
Φ i = m o d ( T p t − t 0 , i , 1 )
足部触地检测
这部分可以参考MIT的论文，Contact Model Fusion for Event-based Locomotion in Unstructred Terrains。理论部分比较多，就不详细展开了。
Regularized Predictive Control
这一章是本文的重点，是控制算法的核心。Regularized Predictive Control在普通MPC算法的基础上，添加人为设计的运动约束，使得机器人具有更好的运动效果。论文中提到：
The philosophy behind RPC is to use our knowledge of robotic and legged systems to inform the optimization.
MIT还有一篇论文是在MPC的基础上添加Whole Body Control来优化机器人的关节输出，两个方法都有可取之处，不过在我看来，如果四足的运动控制板性能有限，可以考虑选择一个计算量需求小一点的算法，来进行整体的权衡。 （说的就是Up Board）
选择合适的Regular Heuristics Cost Function可以提高优化的结果并提升计算速度，但是若选择了不合适的函数，则可能只能求得局部最优解，甚至无法求解。为了避免手工设计的Heuristics Cost Function具有缺陷，后文作者使用一种基于学习的方法来得到更优的Heuristics Cost Function
MPC Control
这一节主要介绍MPC算法。
为了达到实时的MPC控制，我们需要尽量减少计算量，同时又要保证计算结果的有效性，因此在这里选择了简化模型的方法。
在该模型中，机器人状态定义如下：
x = [ p Θ p ˙ Θ ˙ ] \bold{x} = \left[ \begin{array}{l}
\bold{p} \\
\bold{\Theta} \\
\dot{\bold{p}} \\
\dot{\bold{\Theta}}
\end{array} \right] x = ⎣ ⎢ ⎢ ⎢ ⎡ p Θ p ˙ Θ ˙ ⎦ ⎥ ⎥ ⎥ ⎤
其中，p \bold{p} p Θ \bold{\Theta} Θ
u = [ r 1 f 1 . . . r F f F ] \bold{u} = \left[ \begin{array}{l}
\bold{r}_1 \\
\bold{f}_1 \\
... \\
\bold{r}_F \\
\bold{f}_F
\end{array} \right] u = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ r 1 f 1 . . . r F f F ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
由此得到的机器人化简后离散系统的动力学：
x k + 1 = A ( Δ t k ) x k + B ( Δ t k ) h ( x k , u k , Φ k ) + d ( Δ t k ) \bold{x}_{k+1} = \bold{A}(\Delta t_k)\bold{x}_k + \bold{B}(\Delta t_k)h(\bold{x}_k, \bold{u}_k, \bold{\Phi}_k) + \bold{d}(\Delta t_k)
x k + 1 = A ( Δ t k ) x k + B ( Δ t k ) h ( x k , u k , Φ k ) + d ( Δ t k )
其中：
A ( Δ t k ) = [ I 6 Δ t k I 6 0 6 I 6 ] , B ( Δ t k ) = [ Δ t k 2 2 I − 1 Δ t k I − 1 ] , d ( Δ t k ) = [ Δ t k 2 2 a g Δ t k a g ] , a g = [ g T 0 3 × 1 T ] T \bold{A}(\Delta t_k) = \left[ \begin{array}{l} \bold{I}_6 & \Delta t_k \bold{I}_6 \\ \bold{0}_6 & \bold{I}_6 \end{array} \right],
\bold{B}(\Delta t_k) = \left[ \begin{array}{l} \tfrac{\Delta t_k^2}{2}\bold{I}^{-1} \\ \Delta t_k \bold{I}^{-1} \end{array} \right],
\bold{d}(\Delta t_k) = \left[ \begin{array}{l} \tfrac{\Delta t_k^2}{2} \bold{a}_g \\ \Delta t_k \bold{a}_g \end{array} \right],
\bold{a}_g = [\bold{g}^T \ \bold{0}_{3 \times 1}^T]^T A ( Δ t k ) = [ I 6 0 6 Δ t k I 6 I 6 ] , B ( Δ t k ) = [ 2 Δ t k 2 I − 1 Δ t k I − 1 ] , d ( Δ t k ) = [ 2 Δ t k 2 a g Δ t k a g ] , a g = [ g T 0 3 × 1 T ] T
h ( x k , u k , Φ k ) h(\bold{x}_k, \bold{u}_k, \bold{\Phi}_k) h ( x k , u k , Φ k )
在前文提到过，机器人假设欧拉角中roll和pitch角很小，由此简化了动力学模型。MPC就是在前述的动力学方程上加上约束得到的。比如足部力需要满足摩擦角约束，比如足部力必须指向地面之类的，再通过非线性求解器得到输出控制量，进行机器人控制。
Regularized MPC
为了进一步优化MPC表现，作者提出了对常规MPC添加Cost Function的方法来改善结果。而Cost Function是通过学习方法得到的。我个人对这个部分不感兴趣，所以没有深入研究。
