本次作业只有两个Part，但是难度上升很多，我做的结果也有点小问题，需要后续修改。

Part 1: 静态逆向运动学

课程中介绍了很多中IK的算法，最简单的是Cyclic Coordinate Descent（CCD），复杂一点的有Gradient Descent、Gauss Newton Method、Damped Gauss Newton Method等。课程中还提到了额外的FABRIK算法等。我在作业中主要实现了前4种方法，其中后三种方法差距不大。

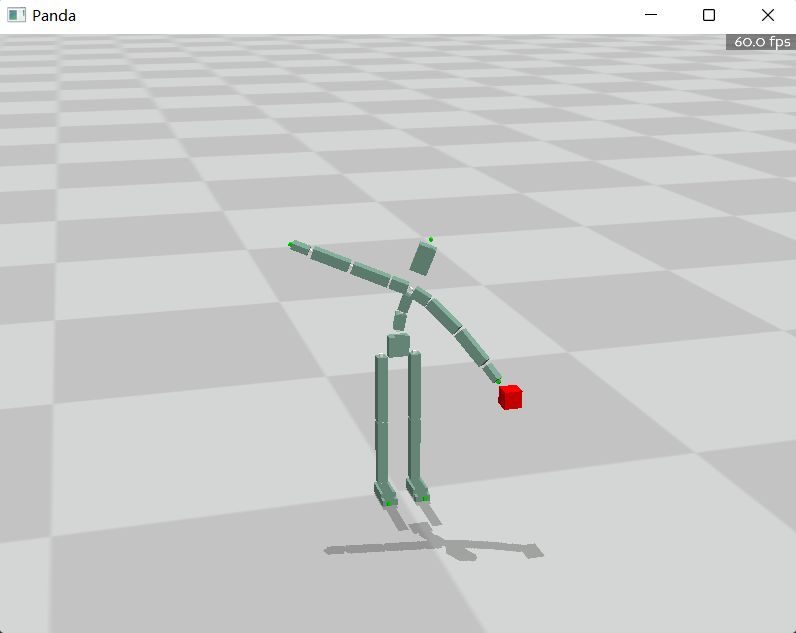
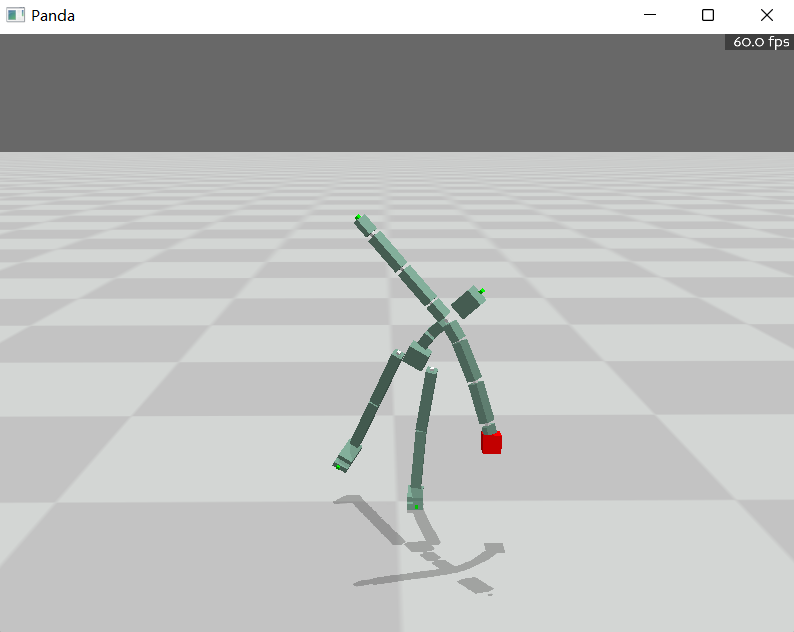
CCD

def cyclicCoordinateDescent(meta_data, joint_positions, joint_orientations, target_pose):
    # 计算 inverse_kinematics 链的信息
    path_offsets, path_positions, path_orientations = getJointPathInfo(meta_data, joint_positions, joint_orientations)

    # CCD 循环
    cnt = 0
    end_index = meta_data.path_name.index(meta_data.end_joint)
    while (np.linalg.norm(joint_positions[meta_data.path[end_index]] - target_pose) >= 1e-2 and cnt <= 10):
        for i in range(end_index):
            current_index = end_index - i - 1
            current_position = path_positions[current_index]
            end_position = path_positions[end_index]
            # delta
            vector_current2end = end_position - current_position
            vector_current2target = target_pose - current_position
            current2end = vector_current2end / np.linalg.norm(vector_current2end)
            current2target = vector_current2target / np.linalg.norm(vector_current2target)

            # 计算轴角
            rotation_radius = np.arccos(np.clip(np.dot(current2end, current2target), -1, 1))
            current_axis = np.cross(current2end, current2target)
            rotation_axis = current_axis / np.linalg.norm(current_axis)
            rotation_vector = R.from_rotvec(rotation_radius * rotation_axis)

            # 计算方位与位置
            path_orientations[current_index] = rotation_vector * path_orientations[current_index]
            path_rotations = []
            path_rotations.append(path_orientations[0])
            # update joint rotations R_{i} = Q_{i-1}^T Q_{i}
            for j in range(len(path_orientations) - 1):
                path_rotations.append(R.inv(path_orientations[j]) * path_orientations[j + 1])
            for j in range(current_index, end_index):
                path_positions[j + 1] = path_positions[j] + path_orientations[j].apply(path_offsets[j + 1])
                if j + 1 < end_index:
                    path_orientations[j + 1] = path_orientations[j] * path_rotations[j + 1]
                else:
                    path_orientations[j + 1] = path_orientations[j]
        cnt += 1
    return path_positions, path_orientations

def applyJointIKToAll(meta_data, joint_positions, joint_orientations, path_positions, path_orientations):
    # print(meta_data.path)
    # print(meta_data.path1)
    # print(meta_data.path2)
    # print(path_orientations)

    # 计算 path_joints 的 rotation
    joint_rotations = R.identity(len(meta_data.joint_name))
    for i in range(len(meta_data.joint_parent)):
        if meta_data.joint_parent[i] == -1:
            joint_rotations[i] = R.from_quat(joint_orientations[i])
        else:
            joint_rotations[i] = R.inv(R.from_quat(joint_orientations[meta_data.joint_parent[i]])) * R.from_quat(joint_orientations[i])

    # # apply IK rotation result
    if len(meta_data.path2) > 1: # we have locked sub chain
        # path_joints 的 forward_kinematics
        # have to set {i}'s joint orientation with {i-1}' orientation
        # because end's joint is not a valid joint
        for i in range(len(meta_data.path2) - 1):
            joint_orientations[meta_data.path2[i + 1]] = path_orientations[i].as_quat()
        joint_orientations[meta_data.path2[-1]] = path_orientations[len(meta_data.path2) - 1].as_quat()
        for i in range(len(meta_data.path1) - 1):
            joint_orientations[meta_data.path[i + len(meta_data.path2)]] = path_orientations[i + len(meta_data.path2)].as_quat()
    else: # we don't have locked sub chain
        # path_joints 的 forward_kinematics
        for j in range(len(meta_data.path)):
            joint_orientations[meta_data.path[j]] = path_orientations[j].as_quat()

    # apply IK position result
    for i in range(len(meta_data.path)):
        joint_positions[meta_data.path[i]] = path_positions[i]

    # 其余 joints 的 forward_kinematics
    for i in range(len(meta_data.joint_parent)):
        if meta_data.joint_parent[i] == -1:
            continue
        if meta_data.joint_name[i] not in meta_data.path_name:
            joint_positions[i] = joint_positions[meta_data.joint_parent[i]] + \
                R.from_quat(joint_orientations[meta_data.joint_parent[i]]).apply(meta_data.joint_initial_position[i] - \
                meta_data.joint_initial_position[meta_data.joint_parent[i]])
            joint_orientations[i] = (R.from_quat(joint_orientations[meta_data.joint_parent[i]]) * joint_rotations[i]).as_quat()

    return joint_positions, joint_orientations

def part1_inverse_kinematics(meta_data, joint_positions, joint_orientations, target_pose):
    """
    完成函数，计算逆运动学
    输入: 
        meta_data: 为了方便，将一些固定信息进行了打包，见上面的meta_data类
        joint_positions: 当前的关节位置，是一个numpy数组，shape为(M, 3)，M为关节数
        joint_orientations: 当前的关节朝向，是一个numpy数组，shape为(M, 4)，M为关节数
        target_pose: 目标位置，是一个numpy数组，shape为(3,)
    输出:
        经过IK后的姿态
        joint_positions: 计算得到的关节位置，是一个numpy数组，shape为(M, 3)，M为关节数
        joint_orientations: 计算得到的关节朝向，是一个numpy数组，shape为(M, 4)，M为关节数
    """
    path_positions, path_orientations = cyclicCoordinateDescent(meta_data, joint_positions, joint_orientations, target_pose)
    joint_positions, joint_orientations = applyJointIKToAll(meta_data, joint_positions, joint_orientations, path_positions, path_orientations)

    return joint_positions, joint_orientations

基于Jacobian矩阵的方法：

def calculateJointAngle(path_orientations):
    path_rotations = []
    path_rotations.append(path_orientations[0])
    # update joint rotations R_{i} = Q_{i-1}^T Q_{i}
    for j in range(len(path_orientations) - 1):
        rot = R.inv(path_orientations[j]) * path_orientations[j + 1]
        path_rotations.append(rot)
    # decompose euler angle
    joint_angle = []
    for r in path_rotations:
        eula = R.from_matrix(r.as_matrix()).as_euler('XYZ', degrees=True)
        joint_angle.append(eula)
    return joint_angle

def calculateJacobian(end_position, joint_angle, path_positions, path_orientations):
    # fill jacobian matrix
    # i'th column = a_{i} x r{i}
    # for XYZ ball joint, use Euler angle to decomposite: R = Rx Ry Rz
    jacobian = []
    print("----")
    print(end_position)
    print("----")

    for i in range(len(joint_angle)):
        # print(path_positions[i], joint_angle[i+1])
        current_position = path_positions[i]
        current_angle = joint_angle[i]
        r = current_position - end_position
        rx = R.from_euler('XYZ', [current_angle[0],  0., 0.], degrees=True)
        rxy = R.from_euler('XYZ', [current_angle[0],  current_angle[1], 0.], degrees=True)
        q_prev = None
        if i == 0:
            q_prev = R.from_quat([ 0. , 0.80976237, 0.53984158, -0.22990426])
        else:
            q_prev = path_orientations[i-1]
        ax = q_prev.apply(np.array([1., 0., 0.]).reshape(-1, 3))
        ay = q_prev.apply(rx.apply(np.array([0., 1., 0.]).reshape(-1, 3)))
        az = q_prev.apply(rxy.apply(np.array([0., 0., 1.]).reshape(-1, 3)))
        jacobian.append(np.cross(ax, r))
        jacobian.append(np.cross(ay, r))
        jacobian.append(np.cross(az, r))
    jacobian = np.concatenate(jacobian, axis=0).transpose()
    return jacobian

def calculateJointPathInJacobian(theta, end_index, path_offsets, path_positions, path_orientations):
    path_rotations = []
    theta = theta.reshape(-1,3)
    for i in range(len(theta)):
        eula = theta[i]
        path_rotations.append(R.from_euler('XYZ', eula, degrees=True))

    print(end_index, len(path_positions), len(path_rotations))

    # update joint rotations R_{i} = Q_{i-1}^T Q_{i}
    # path_orientations[0] = path_rotations[0]
    for j in range(end_index):
        path_positions[j + 1] = path_positions[j] + path_orientations[j].apply(path_offsets[j + 1])
        if j + 1 < end_index:
            path_orientations[j + 1] = path_orientations[j] * path_rotations[j + 1]
        else:
            path_orientations[j + 1] = path_orientations[j]
    return path_positions, path_orientations

def gradientDescent(meta_data, joint_positions, joint_orientations, target_pose):
    # 计算 inverse_kinematics 链的信息
    path_offsets, path_positions, path_orientations = getJointPathInfo(meta_data, joint_positions, joint_orientations)

    end_index = meta_data.path_name.index(meta_data.end_joint)
    count = 0
    alpha = 16
    while (np.linalg.norm(joint_positions[meta_data.path[end_index]] - target_pose) >= 1e-2 and count <= 10):
        end_position = path_positions[end_index]
        joint_angle = calculateJointAngle(path_orientations)
        jacobian = calculateJacobian(end_position, joint_angle, path_positions, path_orientations)
        delta = np.array(target_pose - end_position).reshape(3, -1)

        # get all path rotations, convert to XYZ euler angle
        theta = np.concatenate(joint_angle, axis=0).transpose().reshape(-1, 1)

        # theta_i+1 = theta_i - alpha J^T delta 
        delta = alpha * np.dot(jacobian.transpose(), delta)

        print(theta.transpose())
        print(theta.shape)
        print(delta.transpose())
        print(delta.shape)

        theta = theta - delta

        # convert theta back to rotations
        path_positions, path_orientations = calculateJointPathInJacobian(theta, end_index, path_offsets, path_positions, path_orientations)

        alpha = alpha * 0.8
        count = count + 1

    return path_positions, path_orientations

def gaussNewtonMethod(meta_data, joint_positions, joint_orientations, target_pose):
    # 计算 inverse_kinematics 链的信息
    path_offsets, path_positions, path_orientations = getJointPathInfo(meta_data, joint_positions, joint_orientations)

    end_index = meta_data.path_name.index(meta_data.end_joint)
    count = 0
    alpha = 15
    while (np.linalg.norm(joint_positions[meta_data.path[end_index]] - target_pose) >= 1e-2 and count <= 10):
        end_position = path_positions[end_index]
        joint_angle = calculateJointAngle(path_orientations)
        jacobian = calculateJacobian(end_position, joint_angle, path_positions, path_orientations)
        delta = np.array(target_pose - end_position).reshape(3, -1)

        # get all path rotations, convert to XYZ euler angle
        theta = np.concatenate(joint_angle, axis=0).transpose().reshape(-1, 1)

        # theta = theta_0 - alpha J^T (JJ^T)^-1 delta
        temp = np.linalg.inv(np.dot(jacobian, jacobian.transpose()))
        temp = np.dot(jacobian.transpose(), temp)
        delta = alpha * np.dot(temp, delta)
        theta = theta - delta

        # convert theta back to rotations
        path_positions, path_orientations = calculateJointPathInJacobian(theta, end_index, path_offsets, path_positions, path_orientations)

        alpha = alpha * 0.95
        count = count + 1
    return path_positions, path_orientations

def dampedGaussNewtonMethod(meta_data, joint_positions, joint_orientations, target_pose):
    # 计算 inverse_kinematics 链的信息
    path_offsets, path_positions, path_orientations = getJointPathInfo(meta_data, joint_positions, joint_orientations)
    # theta = theta_0 - alpha J^T (JJ^T + lambda W)^-1 delta

    end_index = meta_data.path_name.index(meta_data.end_joint)
    count = 0
    alpha = 15
    lambda_ = 0.05
    while (np.linalg.norm(joint_positions[meta_data.path[end_index]] - target_pose) >= 1e-2 and count <= 10):
        end_position = path_positions[end_index]
        joint_angle = calculateJointAngle(path_orientations)
        jacobian = calculateJacobian(end_position, joint_angle, path_positions, path_orientations)
        delta = np.array(target_pose - end_position).reshape(3, -1)

        # get all path rotations, convert to XYZ euler angle
        theta = np.concatenate(joint_angle, axis=0).transpose().reshape(-1, 1)

        # theta = theta_0 - alpha J^T (JJ^T + lambda W)^-1 delta
        temp_1 = np.dot(jacobian, jacobian.transpose())
        temp_1 = temp_1 + lambda_ * np.ones(temp_1.shape)
        temp = np.linalg.inv(temp_1)
        temp = np.dot(jacobian.transpose(), temp)
        delta = alpha * np.dot(temp, delta)
        theta = theta - delta

        # convert theta back to rotations
        path_positions, path_orientations = calculateJointPathInJacobian(theta, end_index, path_offsets, path_positions, path_orientations)

        alpha = alpha * 0.95
        count = count + 1
    return path_positions, path_orientations

我写的Jacobian方法里有点小问题，具体来说就是对于Part 2的作业无法适用，但是在静态解算时并没有问题。

Part 2: 逆向运动学+bvh

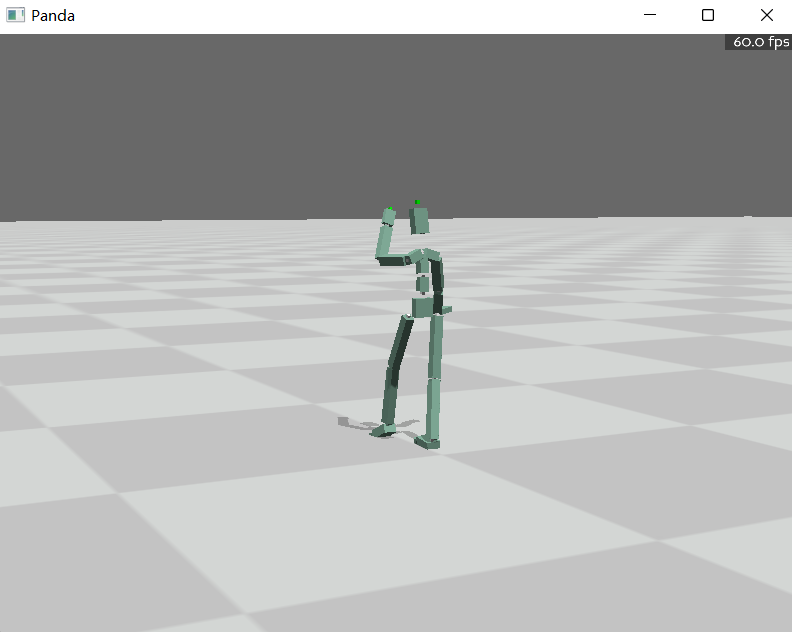
可以看到，作业1中走路的小人变成了看手机走路，说明IK成功。

def part2_inverse_kinematics(meta_data, joint_positions, joint_orientations, relative_x, relative_z, target_height):
    """
    输入lWrist相对于RootJoint前进方向的xz偏移，以及目标高度，IK以外的部分与bvh一致
    """
    target_pose = np.array([joint_positions[0][0] + relative_x, target_height, joint_positions[0][2] + relative_z])
    path_positions, path_orientations = cyclicCoordinateDescent(meta_data, joint_positions, joint_orientations, target_pose)
    joint_positions, joint_orientations = applyJointIKToAll(meta_data, joint_positions, joint_orientations, path_positions, path_orientations)

    return joint_positions, joint_orientations

Part 3(选做)： 两个目标的逆向运动学

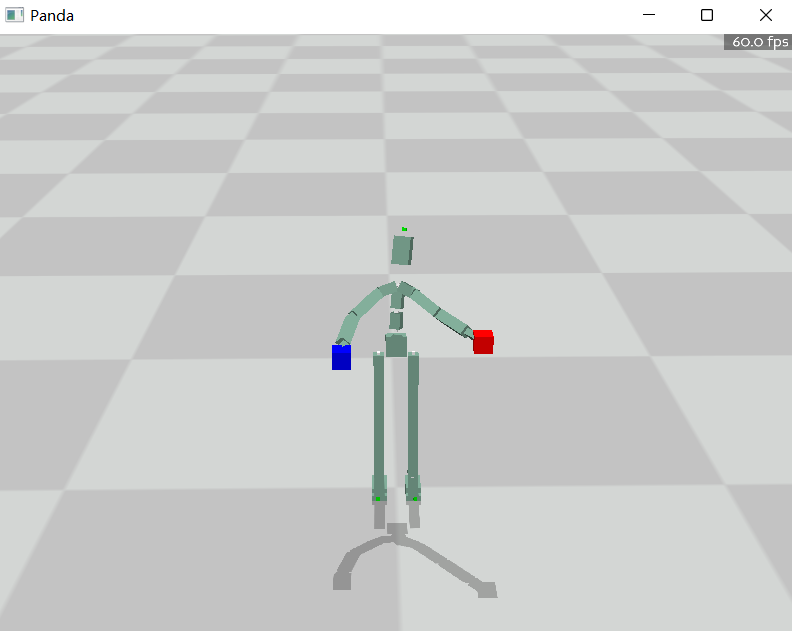
这个部分作业我选择了一个暴力迭代的方法，不论怎么样，就迭代10轮，CCD与Jacobian方法均可得到比较好的效果。CCD方法比Jacobian方法还是快很多。

def bonus_inverse_kinematics(meta_data, joint_positions, joint_orientations, left_target_pose, right_target_pose):
    """
    输入左手和右手的目标位置，固定左脚，完成函数，计算逆运动学
    """
    count = 0
    while count < 10:
        # left target
        meta_data_l = MetaData(meta_data.joint_name, meta_data.joint_parent, meta_data.joint_initial_position, 'RootJoint', 'lWrist_end')
        path_positions_l, path_orientations_l = gradientDescent(meta_data_l, joint_positions, joint_orientations, left_target_pose)
        joint_positions, joint_orientations = applyJointIKToAll(meta_data_l, joint_positions, joint_orientations, path_positions_l, path_orientations_l)

        # right target
        meta_data_r = MetaData(meta_data.joint_name, meta_data.joint_parent, meta_data.joint_initial_position, 'RootJoint', 'rWrist_end')
        path_positions_r, path_orientations_r = gradientDescent(meta_data_r, joint_positions, joint_orientations, right_target_pose)
        joint_positions, joint_orientations = applyJointIKToAll(meta_data_r, joint_positions, joint_orientations, path_positions_r, path_orientations_r)

        count += 1
    
    return joint_positions, joint_orientations