上一篇文章中有一个细节没有提到，就是机器人跳跃到空中的时候，什么时候将腿摆动到期望的位置。作者的方法是，等机器人腾空一小段时间后，这个时候机器人有一定高度后，将腿缩短，然后向前摆动到期望的位置，再将腿伸长，避免足端摆动时意外触地，导致机器人绊倒。同时，为了进行机器人的位置控制，可以使用下述公式来计算期望的机器人速度：

$$\dot{x}_d=min[k(x-x_d),\dot{x}_{max}]$$

这篇文章主要介绍从2D推广到3D的跳跃机器人控制。

Hopping in Three Dimensions

相比起2D的情况，3D多了什么呢？多出了一个平面以及一个旋转。经过作者分析，发现2D的平面机器人运动控制可以扩展到3D机器人的运动控制上。

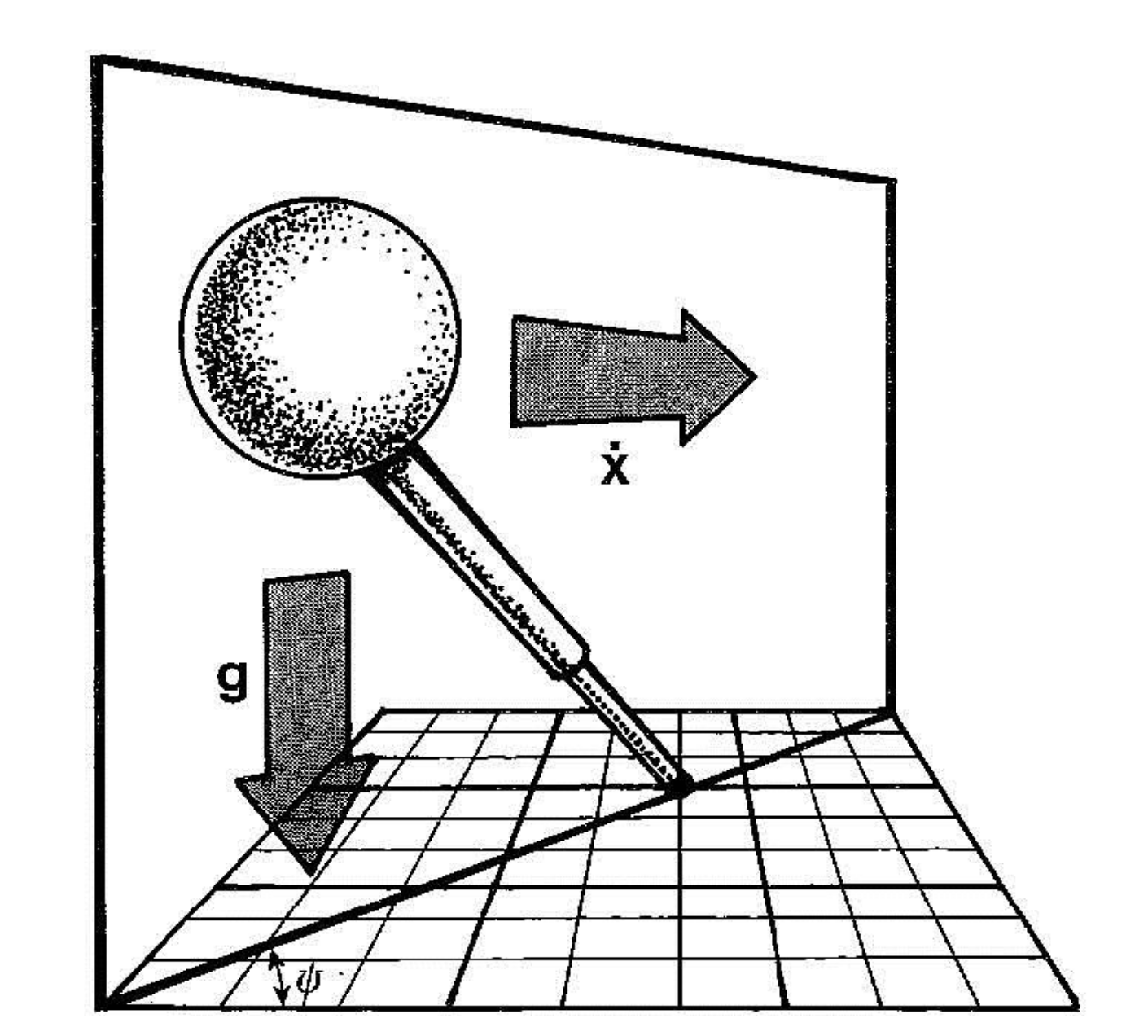
Balance in Three Dimensions

首先先不考虑绕Z轴的旋转控制，将三维空间拆分成XZ平面与YZ平面，在每个平面上，都可以使用2D的平面机器人控制算法来控制机器人运动。机器人的速度可以用以下公式来更新：

$$\dot{\boldsymbol{x}}_{i+1}=\dot{\boldsymbol{x}}_i + \Delta\dot{\boldsymbol{x}}$$

3D One-Legged Hopping Robot

为了实现机器人的控制，作者设计了一个单足3D跳跃机器人，腿部设计与平面跳跃机器人基本相同，但是可以进行足端的3D运动。这个结构是通过两个线性伸缩杆结合Hip关节的球铰实现的。

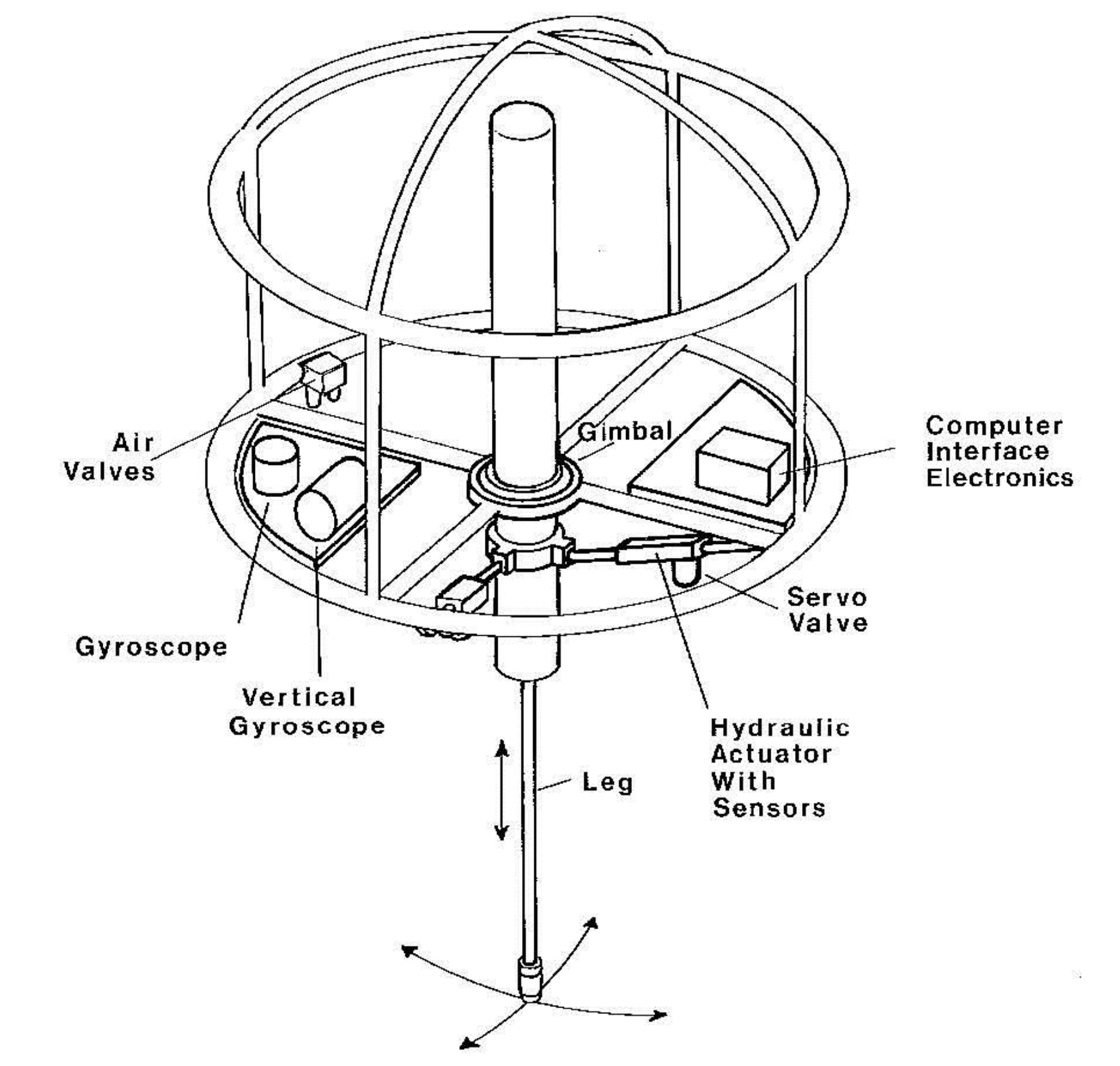
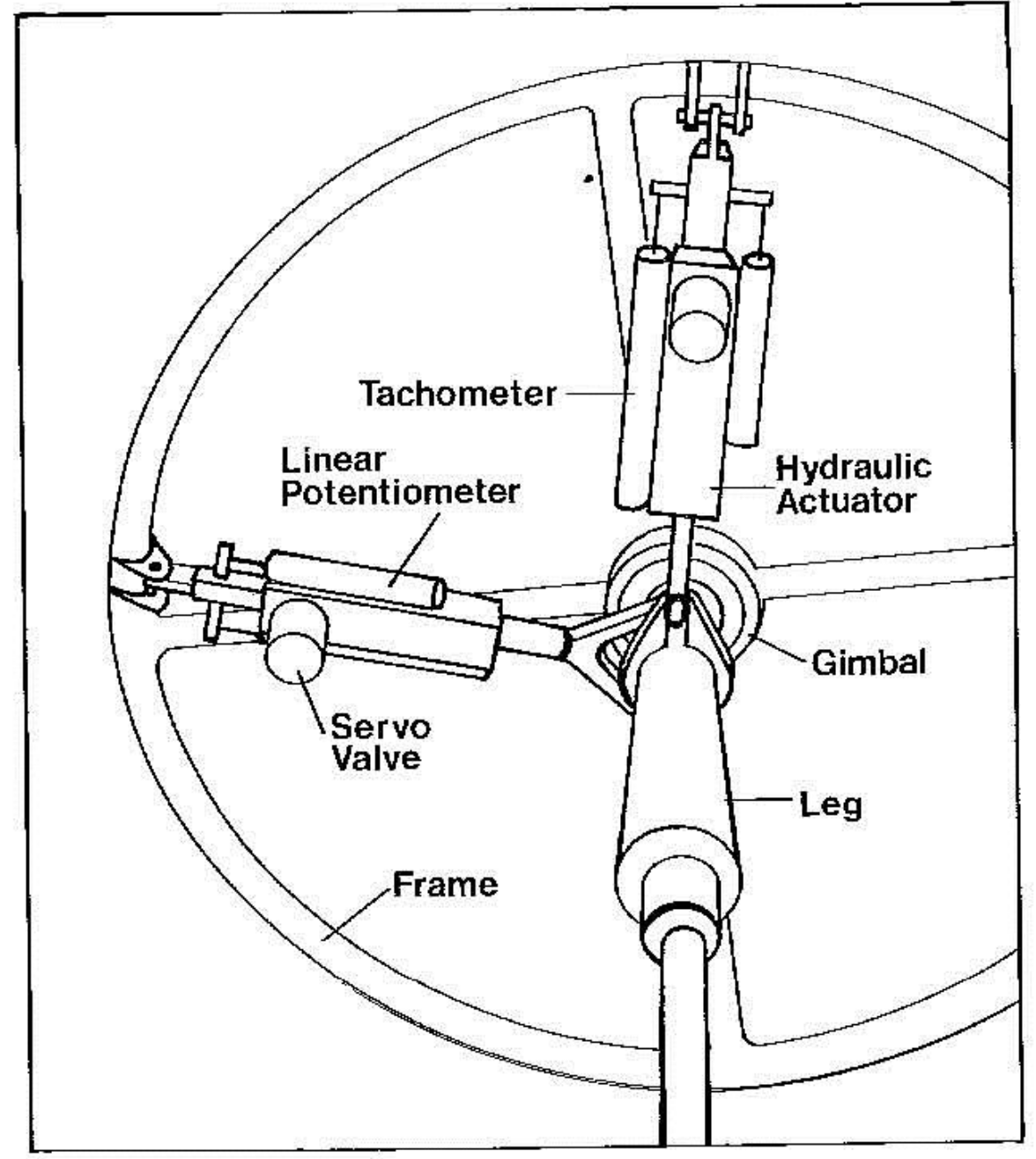
Control System for 3D One-Legged Machine

通过下述几个公式，就可以实现3D跳跃机器人控制，这个控制算法和2D的情况一模一样，唯一的区别就是控制量变成的向量的形式。

$$\boldsymbol{x}_{f0}=\dot{\boldsymbol{x}}T_s/2$$

$$\boldsymbol{x}_{f\Delta}=k_{\dot{\boldsymbol{x}}}(\dot{\boldsymbol{x}}-\dot{\boldsymbol{x}}_d)$$

$$\boldsymbol{x}_f = \dot{\boldsymbol{x}}T_s/2 + k_{\dot{\boldsymbol{x}}}(\dot{\boldsymbol{x}}-\dot{\boldsymbol{x}}_d)$$

$$\boldsymbol{\tau} = -k_p(\boldsymbol{\phi}-\boldsymbol{\phi}_d)-k_v\dot{\boldsymbol{\phi}}$$

虽然这个机器人没有设计用于生成绕Z轴的力矩的机构，用于控制机器人的朝向，但是通过一些技巧，也可以间接实现机器人的转向控制。这个转向力矩与足端提供的力与足端的落地位置有关，可以通过一些额外的机器人运动来产生很小的转向力矩，使得机器人一点点转向。

最后，为了实现机器人位置控制，可以用下述公式来产生机器人的期望运动速度：

$$\dot{\boldsymbol{x}}_d=min[-k_p(\boldsymbol{x}-\boldsymbol{x}_d)-k_v\dot{\boldsymbol{x}},\dot{\boldsymbol{x}}_{max}]$$