相机成像的基本数学原理

1 基础理论

本小节主要介绍相机成像的基本数学原理（Pinhole模型），以及双目成像的原理。这个部分的理论主要参考¹²。

1.1 基本成像模型

相机成像模型如下图所示，世界坐标系\{x_w y_w z_w\}下的一个点\bold{p}在相机坐标系\{x_c y_c z_c\}的Pinhole进行投影，落在焦距为f的图像平面上，在图像坐标系\{x_i y_i\}下的位置\bold{p}_i。具体的坐标系定义可以看下图：

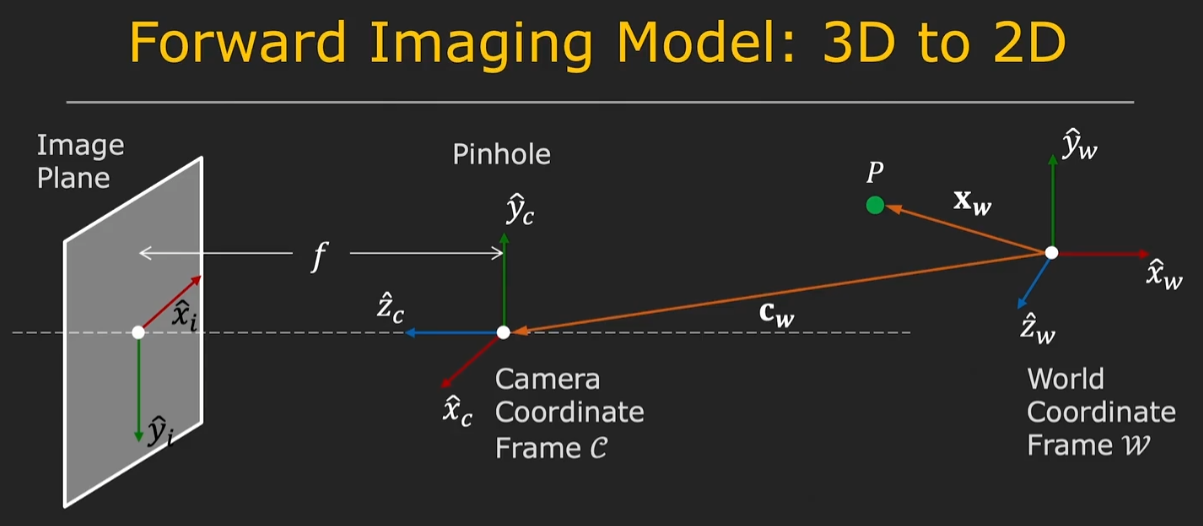
相机成像模型

我们定义下述变量：
\begin{equation} \bold{x}_i = \begin{bmatrix} x_i \\ y_i \end{bmatrix}, \bold{x}_c = \begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix}, \bold{x}_w = \begin{bmatrix} x_w \\ y_w \\ z_w \end{bmatrix} \end{equation}
根据相机焦距得到的基本投影关系为：
\begin{equation} \begin{aligned} \frac{x_i}{f} & =\frac{x_c}{z_c}, \\ \frac{y_i}{f} & =\frac{y_c}{z_c} \end{aligned} \end{equation}
可以得到：
\begin{equation} \begin{aligned} x_i & =f\frac{x_c}{z_c}, \\ y_i & =f\frac{y_c}{z_c} \end{aligned} \end{equation}
虽然我们定义的\bold{p}_i是浮点数，且坐标系原点在图像中心，在针孔的正后方，但是实际的相机传感器并不是这样的，且采集图像的原点一般在左下角，如下图所示：

Image Plane to Image Sensor Mapping

为了解决这两个定义的变换问题，定义m_x，m_y为像素密度，o_x，o_y为图像像素到图像中心的位置。图像的像素位置与图像平面的投影点的关系如下：
\begin{equation} \begin{aligned} u & =m_x x_i=m_x f \frac{x_c}{z_c} + o_x, \\ v & =m_y y_i=m_y f \frac{y_c}{z_c} + o_y \end{aligned} \end{equation}

1.2 相机内参模型

将上述公式进行调整，我们可以得到投影变换方程：
\begin{equation} \begin{aligned} u & =f_x \frac{x_c}{z_c} + o_x, \\ v & =f_y \frac{y_c}{z_c} + o_y \end{aligned} \end{equation}
在这个公式里，(f_x,f_y,o_x,o_y)为相机内参，单个摄像机标定的目标就求这些内参。为了方便后续表达与计算，在这里引入了齐次坐标，定义如下：
\begin{equation} \begin{aligned} \bold{u} & = \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} =\begin{bmatrix} \widetilde{w}u \\ \widetilde{w}v \\ \widetilde{w} \end{bmatrix} =\begin{bmatrix} \widetilde{u} \\ \widetilde{v} \\ \widetilde{w} \end{bmatrix}, \\ \bold{x} & = \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} =\begin{bmatrix} \widetilde{w}x \\ \widetilde{w}y \\ \widetilde{w}z \\ \widetilde{w} \end{bmatrix} =\begin{bmatrix} \widetilde{x} \\ \widetilde{y} \\ \widetilde{z} \\ \widetilde{w} \end{bmatrix} \end{aligned} \end{equation}
将齐次坐标代入投影变换方程可得：
\begin{equation} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} =\begin{bmatrix} \widetilde{u} \\ \widetilde{v} \\ \widetilde{w} \end{bmatrix} =\begin{bmatrix} f_x x_c + o_x z_c \\ f_y x_c + o_y z_c \\ z_c \end{bmatrix} =\begin{bmatrix} f_x & 0 & o_x & 0 \\ 0 & f_y & o_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_c \\ y_c \\ z_c \\ 1 \end{bmatrix} =M_{int} \bold{x} \end{equation}
我们得到了线性投影模型（Linear Projection Model）。其中相机内参矩阵定义为：
\begin{equation} K=\begin{bmatrix} f_x & 0 & o_x \\ 0 & f_y & o_y \\ 0 & 0 & 0 \end{bmatrix} \end{equation}

1.3 相机外参模型

相机外部参数指的是世界坐标系\{x_w y_w z_w\}到相机坐标系\{x_c y_c z_c\}的变换，包括旋转矩阵R和位移t。旋转矩阵定义为：
\begin{equation} ^cR_w=\begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} =\begin{bmatrix} ^wx_c \\ ^wy_c \\ ^wz_c \end{bmatrix} =\begin{bmatrix} ^cx_w & ^cy_w & ^cz_w \end{bmatrix} \end{equation}
代入坐标变换关系，可得：
\begin{equation} \bold{x}_c = R(\bold{x}_w-\bold{c}_w) = R\bold{x}_w - R\bold{c}_w = R\bold{x}_w + \bold{t} \end{equation}
使用齐次坐标表示，可得：
\begin{equation} \widetilde{\bold{x}} =\begin{bmatrix} x_c \\ y_c \\ z_c \\ 1 \end{bmatrix} =\begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} \end{equation}
我们定义M_{ext}=\begin{bmatrix} R & t \\ 0 & 1\end{bmatrix}为相机的外参矩阵（Extrinsic Parameters）。

1.4 相机标定

利用上述模型，我们即可进行相机的内参标定。首先我们需要一个已知的物体模型，使用相机采集这个物体的图像，其次我们需要找到图像中对应点的世界坐标，如下图所示：

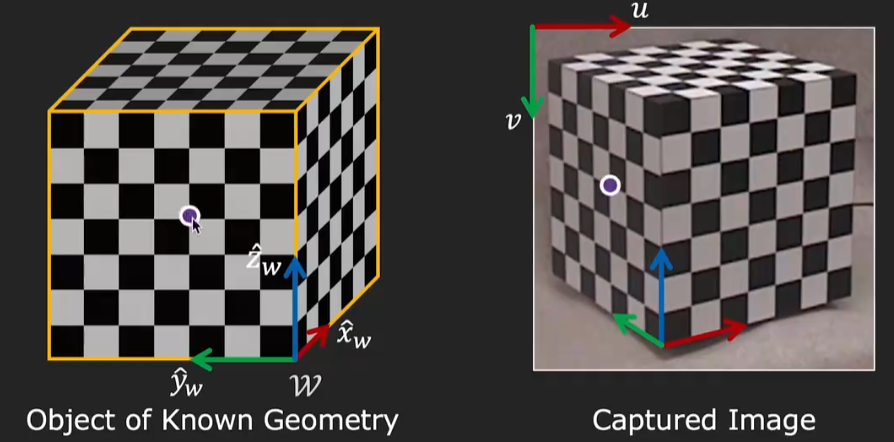
相机标定过程

最后我们需要通过优化方法来计算相机的内外参数。
\begin{equation} \begin{aligned} \begin{bmatrix} u^{i} \\ v{i} \\ 1 \end{bmatrix} & = \begin{bmatrix} f_x & 0 & o_x & 0 \\ 0 & f_y & o_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} \\ & = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} = P \bold{x} \end{aligned} \end{equation}
将上式展开可以得到：
\begin{equation} \begin{aligned} u^i & = \frac{p_{11} x_{w}^{i} + p_{12} y_{w}^{i} + p_{13} z_{w}^{i} + p_{14} }{p_{31} x_{w}^{i} + p_{32} y_{w}^{i} + p_{33} z_{w}^{i} + p_{34} }, \\ v^i & = \frac{p_{21} x_{w}^{i} + p_{22} y_{w}^{i} + p_{23} z_{w}^{i} + p_{24} }{p_{31} x_{w}^{i} + p_{32} y_{w}^{i} + p_{33} z_{w}^{i} + p_{34} } \end{aligned} \end{equation}

将图片中所有点组成的方程进行重新排列，我们得到下面的方程：
\begin{equation} \begin{aligned} \begin{bmatrix} x_w^1 & y_w^1 & z_w^1 & 1 & 0 & 0 & 0 & 0 & -u_1 x_w^1 & -u_1 y_w^1 & -u_1 z_w^1 & -u_1 \\ 0 & 0 & 0 & 0 & x_w^1 & y_w^1 & z_w^1 & 1 & -v_1 x_w^1 & -v_1 y_w^1 & -v_1 z_w^1 & -v_1\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_w^n & y_w^n & z_w^n & 1 & 0 & 0 & 0 & 0 & -u_n x_w^n & -u_n y_w^n & -u_n z_w^n & -u_n \\ 0 & 0 & 0 & 0 & x_w^n & y_w^n & z_w^n & 1 & -v_n x_w^n & -v_n y_w^n & -v_n z_w^n & -v_n \end{bmatrix} \begin{bmatrix} p_{11} \\ p_{12} \\ p_{13} \\ p_{14} \\ p_{21} \\ p_{22} \\ p_{23} \\ p_{24} \\ p_{31} \\ p_{32} \\ p_{33} \\ p_{34} \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \end{aligned} \end{equation}
可以将其表示为：
\begin{equation} \begin{aligned} A \bold{p} = 0 \end{aligned} \end{equation}
为了使解唯一，我们添加\begin{Vmatrix}p\end{Vmatrix}^2=1的约束，问题转变为：
\begin{equation} \begin{aligned} \mathop{\min}_{\bold{p}} \begin{Vmatrix}A\bold{p}\end{Vmatrix}^2, s.t. \begin{Vmatrix}p\end{Vmatrix}^2=1 \end{aligned} \end{equation}
这个问题可以使用拉格朗日法（Lagrange）来解决，定义拉格朗日函数L(\bold{p},\lambda)=\frac{1}{2} \bold{p}^T A^T A \bold{p} - \frac{1}{2} \lambda(\bold{p}^T \bold{p} - 1)可以通过求解这个方程的最小值来解决等式约束问题，我们对\bold{p}求偏导并令导数为零（最小值点的必要条件）：
\begin{equation} \begin{aligned} \nabla_{\bold{p}} L(\bold{p}, \lambda) = A^T A \bold{p} - \lambda \bold{p} = 0 \end{aligned} \end{equation}
求解这个方程即可得到\bold{p}，进行重新排列后可以得到参数矩阵P。取出P的前三列构成矩阵，可以得到下述特性：
\begin{equation} \begin{aligned} \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & p_{33} \end{bmatrix} =\begin{bmatrix} f_x & 0 & o_x \\ 0 & f_y & o_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} \end{aligned} \end{equation}
上述矩阵可以使用QR分解拆分得到左侧的两个矩阵，包括的相机的内参矩阵和旋转矩阵，在对P的最后一列进行处理，就可以得到\bold{t}：
\begin{equation} \begin{aligned} \begin{bmatrix} p_{14} \\ p_{24} \\ p_{34} \end{bmatrix} =\begin{bmatrix} f_x & 0 & o_x \\ 0 & f_y & o_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} \Rightarrow \bold{t} = K^{-1} \begin{bmatrix} p_{14} \\ p_{24} \\ p_{34} \end{bmatrix} \end{aligned} \end{equation}

1.5 立体视觉标定

在进行后续计算时，我们假定相机的内参(f_x,f_y,o_x,o_y)已知，并且我们从左右两个相机采集的图像中找到了对应的点（手工或通过算法），随后我们通过上述数据估计两个相机的外参矩阵，然后使用相机的内参与外参来计算采集图像的深度图。双目成像的示意图如下所示：

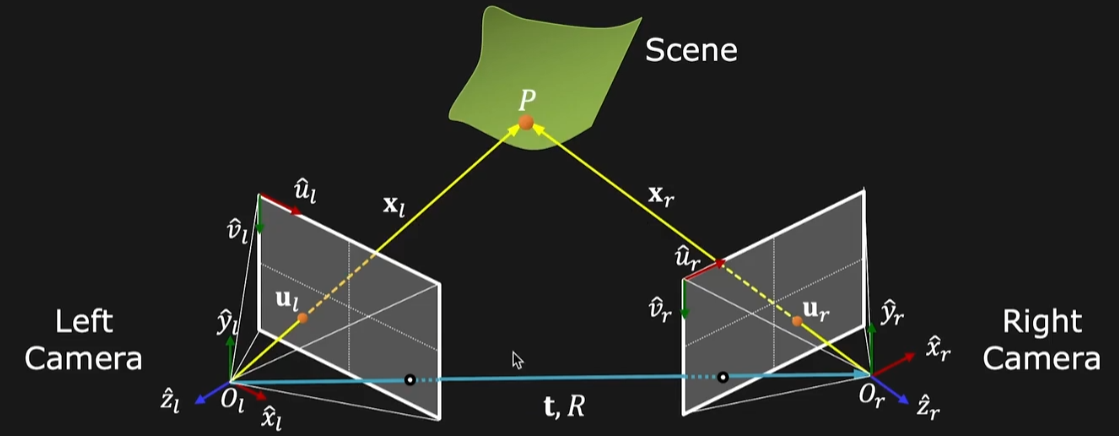
双目相机成像

为了进行相机参数估计，在这里引入了Epipolar Geometry，每个Epipolar Plane由O_l,O_r,P构成。根据三角形约束，我们可以得到下述公式，称为Epipolar Constraint
\begin{equation} \begin{aligned} \bold{n}=\bold{t} \times \bold{x}_l \Rightarrow \bold{x}_l (\bold{t} \times \bold{x}_l) = 0 \end{aligned} \end{equation}
转换成矩阵乘法：
\begin{equation} \begin{aligned} \begin{bmatrix} x_l & y_l & z_l \end{bmatrix} \begin{bmatrix} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{bmatrix} \begin{bmatrix} x_l \\ y_l \\ z_l \end{bmatrix} = 0 \end{aligned} \end{equation}
根据上述矩阵外参，可以得到：
\begin{equation} \begin{aligned} \begin{bmatrix} x_l \\ y_l \\ z_l \end{bmatrix} = R \begin{bmatrix} x_r \\ y_r \\ z_r \end{bmatrix} + \bold{t} \end{aligned} \end{equation}
将Epipolar Constraint和外参的变换公式结合，可以得到：
\begin{equation} \begin{aligned} \begin{bmatrix} u_l & v_l & 1 \end{bmatrix} z_l K_l^{-T} E K_r^{-1} z_r \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} &= \\ \begin{bmatrix} u_l & v_l & 1 \end{bmatrix} K_l^{-T} E K_r^{-1} \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} & = \\ \begin{bmatrix} u_l & v_l & 1 \end{bmatrix} F \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} & = 0 \end{aligned} \end{equation}

其中F\in\Re^{3 \times 3}矩阵为Fundamental Matrix。对每个像素均有：
\begin{equation} \begin{aligned} \begin{bmatrix} u_l^i & v_l^i & 1 \end{bmatrix} F \begin{bmatrix} u_r^i \\ v_r^i \\ 1 \end{bmatrix} & = 0 \end{aligned} \end{equation}
展开所有公式并重新整理，可以得到：
\begin{equation} \begin{aligned} \begin{bmatrix} u_l^1 u_r^1 & u_l^1 v_r^1 & u_l^1 & v_l^1 u_r^1 & v_l^1 v_r^1 & v_l^1 & u_r^1 & v_r^1 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ u_l^n u_r^n & u_l^n v_r^n & u_l^n & v_l^n u_r^n & v_l^n v_r^n & v_l^n & u_r^n & v_r^n & 1 \end{bmatrix} \begin{bmatrix} f_{11} \\ f_{12} \\ f_{13} \\ f_{21} \\ f_{22} \\ f_{23} \\ f_{31} \\ f_{32} \\ f_{33} \end{bmatrix} =\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \end{aligned} \end{equation}
为了保证解的唯一性，我们添加约束\begin{Vmatrix}f\end{Vmatrix}^2=1。通过求解下述优化问题，即可得到Fundamental Matrix，再利用E=K_l^T F K_r来计算相机外参，完成标定：
\begin{equation} \begin{aligned} \mathop{\min}_{\bold{f}} \begin{Vmatrix}A\bold{f}\end{Vmatrix}^2, s.t. \begin{Vmatrix}f\end{Vmatrix}^2=1 \end{aligned} \end{equation}

1.6 立体视觉深度计算

为了解决立体视觉深度计算的问题，我们首先需要知道两个相机采集的图片是怎么匹配的，比如左侧相机的一个像素对应的右侧相机的匹配线是什么样的，这个部分我们也利用Epipolar Geometry来计算投影后的Epipolar Line，如下图红线所示：

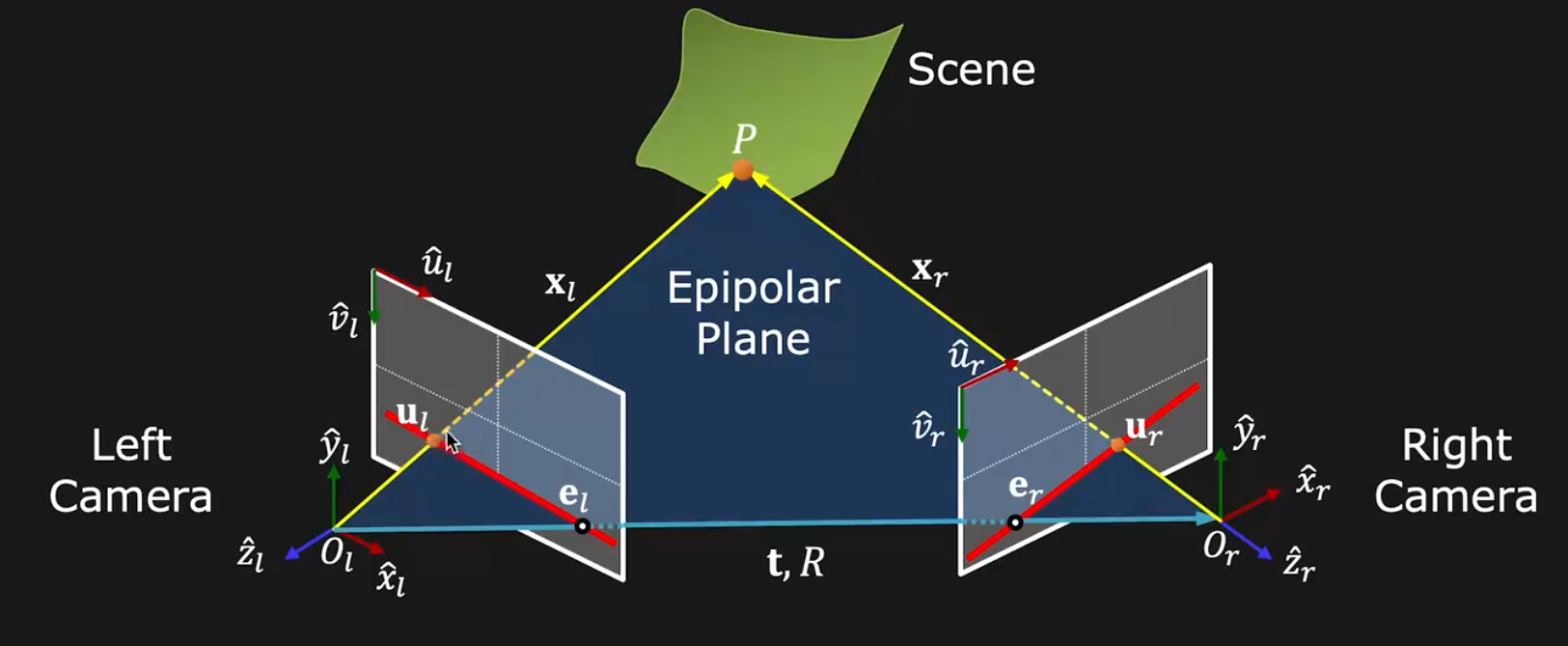
Epipolar Line

\begin{equation} \begin{aligned} \begin{bmatrix} u_l & v_l & 1 \end{bmatrix} \begin{bmatrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{bmatrix} \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} = 0 \end{aligned} \end{equation}
展开后可以得到：

\begin{equation} \begin{aligned} (f_{11} u_l + f_{21} v_l + f_{31}) u_r + (f_{12} u_l + f_{22} v_l + f_{32}) v_r + (f_{13} u_l + f_{23} v_l + f_{33}) &= 0 \Rightarrow \\ a_l u_r + b_l v_r + c_l &= 0, \\ a_r u_l + b_r v_l + c_r &= 0 \end{aligned} \end{equation}
上述直线就是Epipolar Line，分别在左右相机的方程。在这个Epipolar Line上找到两个图像的匹配点后（可以使用SIFT等算法进行匹配），我们就要使用三角关系来计算该点的深度了：

\begin{equation} \begin{aligned} \begin{bmatrix} u_l \\ v_l \\ 1 \end{bmatrix} & = \begin{bmatrix} f_x^l & 0 & o_x^l & 0\\ 0 & f_y^l & o_y^l & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_l \\ y_l \\ z_l \\ 1 \end{bmatrix} , \\ \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} & = \begin{bmatrix} f_x^r & 0 & o_x^r & 0\\ 0 & f_y^r & o_y^r & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_r \\ y_r \\ z_r \\ 1 \end{bmatrix} \end{aligned} \end{equation}

代入相机外参：
\begin{equation} \begin{aligned} \widetilde{u}_l &= K_l T_l \widetilde{x}_r = P_l \widetilde{x}_r \\ \widetilde{u}_r &= M_{int} \widetilde{x}_r \end{aligned} \end{equation}
展开后重新排列可得：
\begin{equation} \begin{aligned} \begin{bmatrix} u_r m_{31} - m_{11} & u_r m_{32} - m_{12} & u_r m_{33} - m_{13} \\ v_r m_{31} - m_{21} & v_r m_{32} - m_{22} & v_r m_{33} - m_{23} \\ u_l p_{31} - p_{11} & u_l p_{32} - p_{12} & u_l p_{33} - p_{13} \\ v_l p_{31} - p_{21} & v_l p_{32} - p_{22} & v_l p_{33} - p_{23} \end{bmatrix} \begin{bmatrix} x_r \\ y_r \\ z_r \end{bmatrix} &= \begin{bmatrix} m_{14} - m_{34} \\ m_{24} - m_{34} \\ p_{14} - p_{34} \\ p_{24} - p_{34} \end{bmatrix} \\ A \begin{bmatrix} x_r \\ y_r \\ z_r \end{bmatrix} &= \bold{b} \end{aligned} \end{equation}

求解方程可得：

\begin{equation} \begin{aligned} \bold{x}_r = (A^T A)^{-1} A^T b \end{aligned} \end{equation}