本章进行并联踝关节的正运动学计算。对于并联机构来说，比较好求逆运动学，而正运动学比较难计算，本章采用数值方法求解正运动学。具体的算法讲解可以看CMU Optimal Control这个课程，老师讲的非常好。

首先先上结论图：
下图是根据运动学建立方程的三维网格曲面，其中与z=0平面相交的点就是方程的解。这个方程比较难求解，但是在定义域内大致单调可导，因此采用数值方法求解。

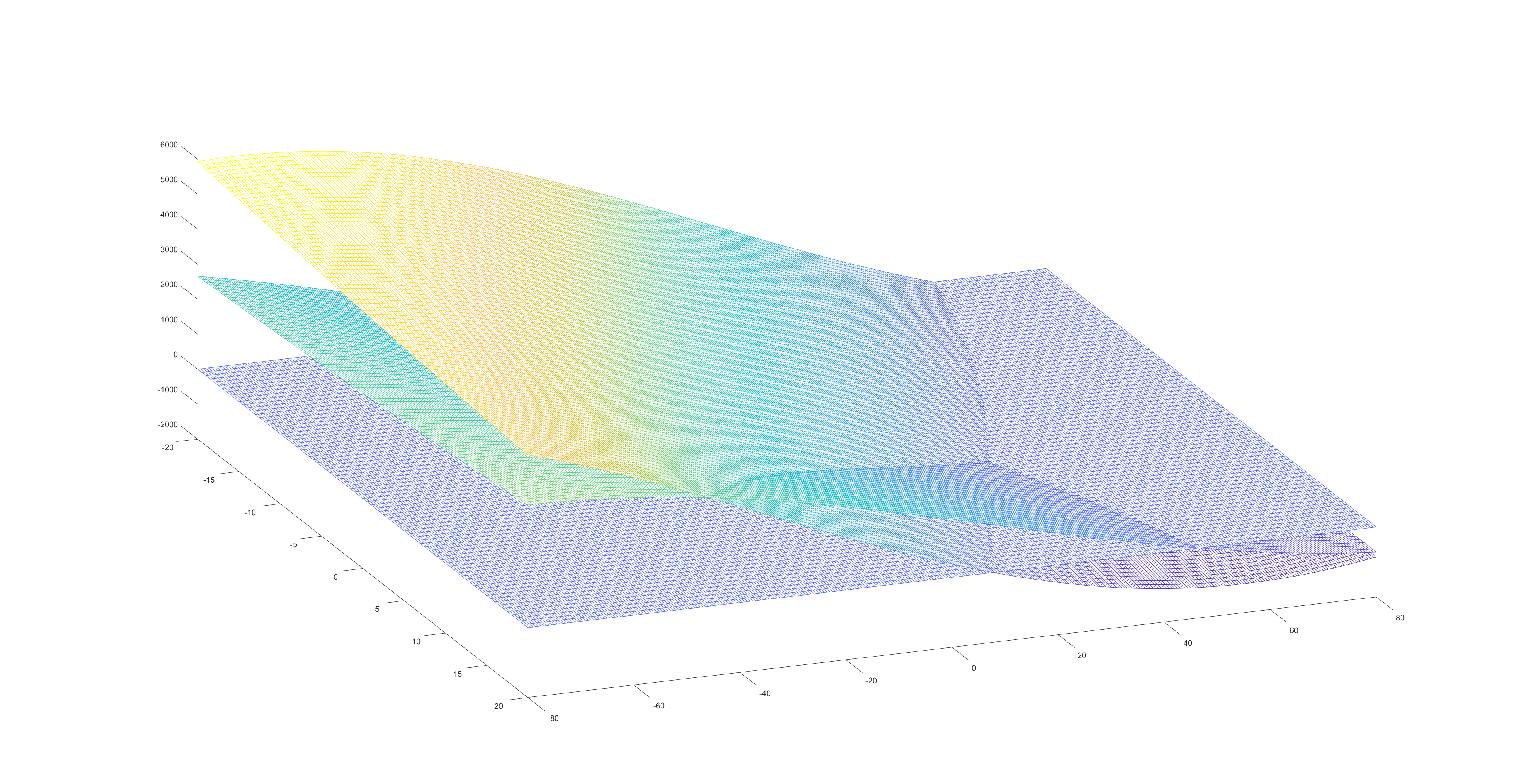
下图中的直线是牛顿法求根的迭代轨迹。在运行5个迭代流程后，解的误差已经下降到1e-6，收敛速度很快：

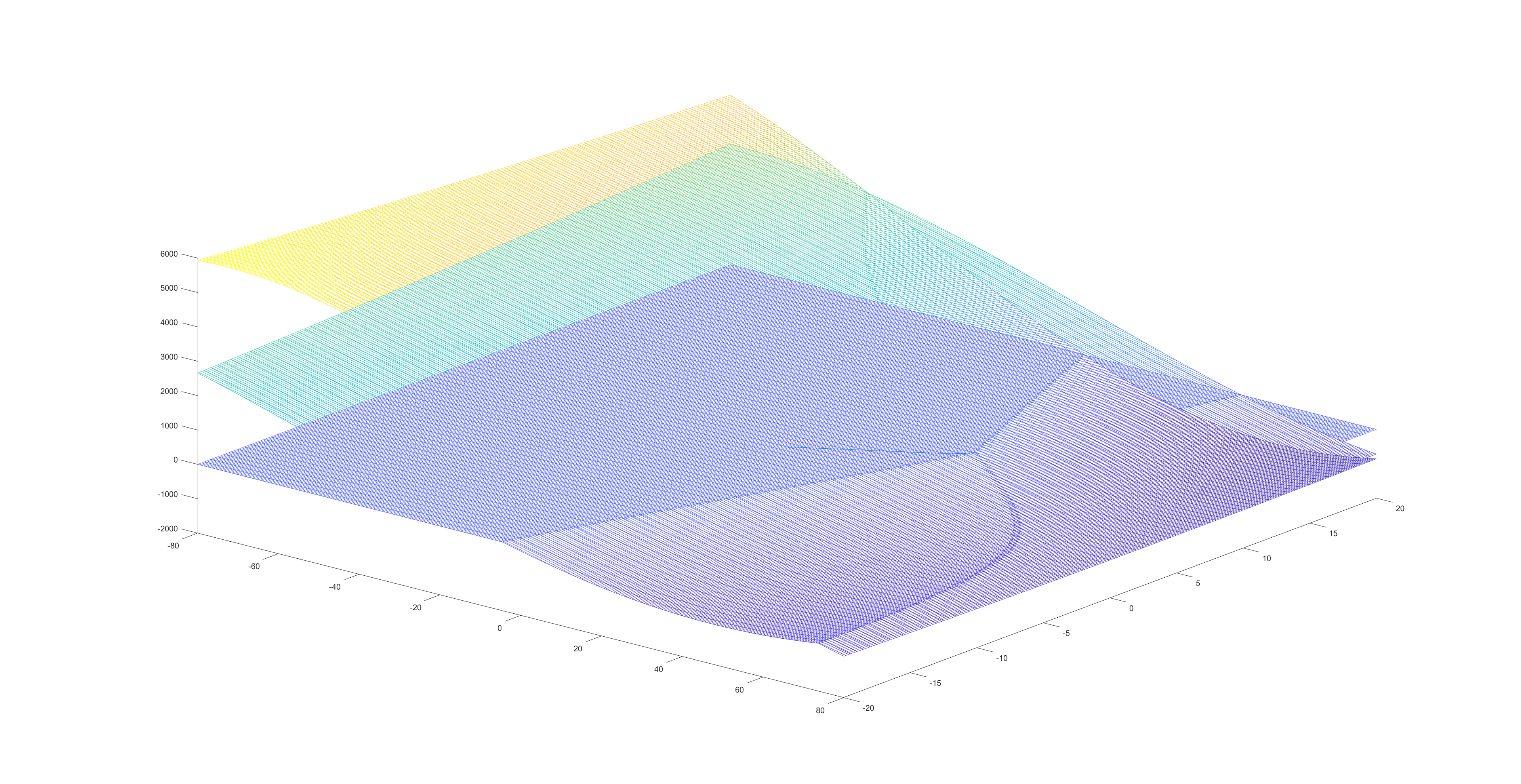
经检验，结果完全符合预期。

具体matlab代码如下：

clear;
clc;

L1 = 25;
d = 69.8 / 2.0;
h1 = 112;
h2 = 65;

[tmL, tmR] = ankle_ik_func(L1, d, h1, h2, 5, 30)

% function mesh
start_x = -20;
step_x = 0.1;
end_x = 20;

start_y = -80;
step_y = 0.1;
end_y = 80;

[tx_mat, ty_mat] = meshgrid(start_x:step_x:end_x, start_y:step_y:end_y);
t1_mat = zeros(size(tx_mat));
t2_mat = zeros(size(tx_mat));
z_mat = zeros(size(tx_mat));
i = 1;
hold on
for tx = start_x:step_x:end_x
    t1_list = start_y:step_y:end_y;
    t2_list = start_y:step_y:end_y;
    z_list = start_y:step_y:end_y;
    k = 1;
    for ty = start_y:step_y:end_y
        result = f(tx / 180 * pi, ty / 180 * pi, d, h1, h2, L1, tmL / 180 * pi, tmR / 180 * pi);
		t1_list(k) = result(1);
		t2_list(k) = result(2);
		z_list(k) = 0;
		k = k + 1;
	end
	t1_mat(:,i) = t1_list;
	t2_mat(:,i) = t2_list;
	z_mat(:,i) = z_list;
	i = i + 1;
end

a = mesh(tx_mat, ty_mat, t1_mat);
% a.EdgeColor(4) = 0.3;
% % a.FaceAlpha = 0.2;
a = mesh(tx_mat, ty_mat, t2_mat);
% a.EdgeColor(4) = 0.3;
% % a.FaceAlpha = 0.2;
a = mesh(tx_mat, ty_mat, z_mat);
% a.EdgeColor(4) = 0.3;
% % a.FaceAlpha = 0.2;

% newton method
txy = [0;0];
tx_list = [txy(1) * 180 / pi];
ty_list = [txy(2) * 180 / pi];
height = [0];
count = 0;
err_v = f(txy(1), txy(2), d, h1, h2, L1, tmL / 180 * pi, tmR / 180 * pi);
err = err_v' * err_v;
err_list = [err];
indexs = [count];
while count < 50 && err > 1e-6
	df_mat = df(txy(1), txy(2), d, h1, h2, L1, tmL / 180 * pi, tmR / 180 * pi);
	J = pinv(df_mat);
	f_ = f(txy(1), txy(2), d, h1, h2, L1, tmL / 180 * pi, tmR / 180 * pi);
	dxy = -J * f_;
	txy = txy + dxy;

	tx_list = [tx_list, txy(1) * 180 / pi];
	ty_list = [ty_list, txy(2) * 180 / pi];
	height = [height, 0];

	% plot3(txy(1), txy(2), 0)
	err_v = f(txy(1), txy(2), d, h1, h2, L1, tmL / 180 * pi, tmR / 180 * pi);
	err = err_v' * err_v;
	count = count + 1;

	err_list = [err_list, err];
	indexs = [indexs, count];
end

plot3(tx_list, ty_list, height, "-")
% plot(indexs, err_list)

tx = txy(1) * 180 / pi
ty = txy(2) * 180 / pi

function result = f(tx, ty, d, h1, h2, L1, tML, tMR)
	res1 = L1^2 + d^2 - d^2*cos(tx) - L1^2*cos(tML)*cos(ty) - L1^2*sin(tML)*sin(ty) + L1*h1*sin(tML) - L1*h1*sin(ty) - d*h1*cos(ty)*sin(tx) + L1*d*cos(tML)*sin(tx)*sin(ty) - L1*d*cos(ty)*sin(tML)*sin(tx);
	res2 = L1^2 + d^2 - d^2*cos(tx) - L1^2*cos(tMR)*cos(ty) - L1^2*sin(tMR)*sin(ty) + L1*h2*sin(tMR) - L1*h2*sin(ty) + d*h2*cos(ty)*sin(tx) - L1*d*cos(tMR)*sin(tx)*sin(ty) + L1*d*cos(ty)*sin(tMR)*sin(tx);
	result = [res1, res2]';
end

function df_mat = df(tx, ty, d, h1, h2, L1, tML, tMR)
	df1_dx1 = d^2*sin(tx) - d*h1*cos(ty)*cos(tx) + L1*d*cos(tML)*cos(tx)*sin(ty) - L1*d*cos(ty)*sin(tML)*cos(tx);
	df2_dx1 = d^2*sin(tx) + d*h2*cos(ty)*cos(tx) - L1*d*cos(tMR)*cos(tx)*sin(ty) + L1*d*cos(ty)*sin(tMR)*cos(tx);

	df1_dx2 = L1^2*cos(tML)*sin(ty) - L1^2*sin(tML)*cos(ty) - L1*h1*cos(ty) + d*h2*sin(ty)*sin(tx) + L1*d*cos(tML)*sin(tx)*cos(ty) + L1*d*sin(ty)*sin(tML)*sin(tx);
	df2_dx2 = L1^2*cos(tMR)*sin(ty) - L1^2*sin(tMR)*cos(ty) - L1*h2*cos(ty) - d*h2*sin(ty)*sin(tx) - L1*d*cos(tMR)*sin(tx)*cos(ty) - L1*d*sin(ty)*sin(tMR)*sin(tx);

	df_mat = [df1_dx1, df1_dx2;df2_dx1, df2_dx2];
end